Duration: 2h 49m | 5 sections | 24 lectures | Video: 1280×720, 44 KHz | 974 MB
Genre: eLearning | Language: English + Sub
Calculus -I (Improper Integral)
What you’ll learn
Students will learn how to find the Laplace Transform of certain functions and its applications in Differential Equations
Requirements
Derivatives, Integrals and Improper Integrals
Description
Ordinary and partial differential equations describe the way certain quantities vary with time, such as the current in an electrical circuit, the oscillations of a vibrating membrane, or the flow of heat through an insulated conductor. These equations are generally coupled with initial conditions that describe the state of the system at time t = 0. A very powerful technique for solving these problems is that of the Laplace transform, which literally transforms the original differential equation into an elementary algebraic expression. This latter can then simply be transformed once again, into the solution of the original problem. This technique is known as the “Laplace transform method.”
We will study the following:
Basic Definition of Laplace Transform and its Existence.
Exponential Order
Sufficient conditions for Existence.
Laplace Transform is a linear Operator.
Laplace Transform of a Constant Function.
Laplace Transform of a Monomial Function.
Laplace Transform of a polynomial Function.
Laplace Transform of a Exponential Function.
Laplace Transform of a Sine and cosine Function.
Laplace Transform of a Hyperbolic Sine and cosine Function.
Laplace Transform of a composition of a Function.
Laplace Transform of a Piece-wise Function.
Laplace Transform by First Translation Theorem.
Unit Step Function.
Laplace Transform by Second Translation Theorem.
Derivatives of Transforms.
Convolution Theorem
Inverse Laplace Transform
Inverse Laplace Transform is a linear Operator.
Inverse Laplace Transform by Partial Fraction.
Inverse Form of First Translation Theorem.
Inverse Form of Second Translation Theorem.
Inverse form of Convolution Theorem.
Application of Laplace Transform.
\n
Who this course is for:Engineers and Mathematicians
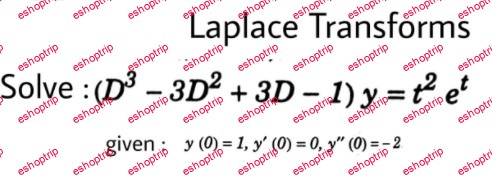










Reviews
There are no reviews yet.